In questo post viene illustrato il funzionamento dell’algoritmo di euclide per il calcolo del Massimo Comun Divisore (MCD) fra due numeri interi. L’algoritmo è presente nel libro Elementi di Euclide (circa 300 a.C.) ma si pensa che già precedentemente fosse conosciuto.

Massimo Comun Divisore

Per prima cosa, ricordiamo la definizione di massimo comun divisore fra due numeri:

Il Massimo Comun Divisore (MCD) è il più grande dei divisori fra i numeri considerati.

Facciamo un esempio per capire bene. Supponiamo di dover calcolare il MCD fra i numeri 6 e 4. Per prima cosa possiamo scomporre i due numeri in fattori primi scrivendo:

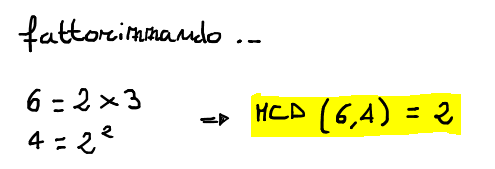
Poichè dobbiamo prendere il più grande dei disivori comuni, notiamo che l’unico in comune è il numero 2. Ciò è ragionavole in quanto sappiamo che l’unico numero per il quale 6 e 4 sono divisibili (la loro divisione intera non produce un resto) è proprio 2.

Euclide tanto tempo fa, ha risolto il problema del calcolo del MCD con un algoritmo che non prevede la fattorizzazione dei numeri. Questo algoritmo è applicabile solo per il calcolo fra due numeri interi.

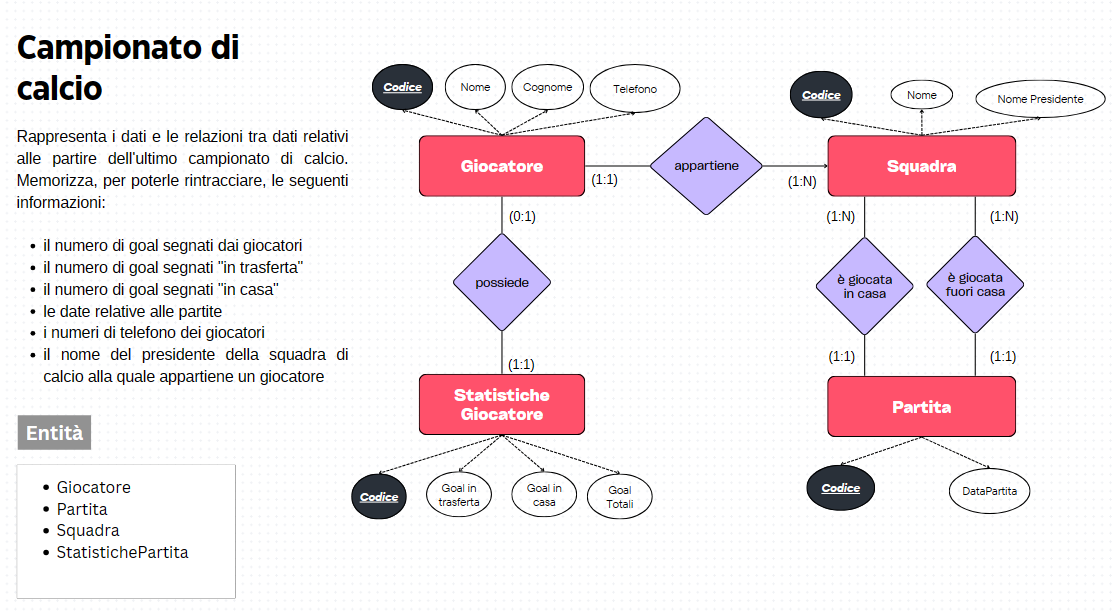
Progetto

Dal punto di vista informatico questo algoritmo può essere implementato come una funzione che prende in input due valori corrispondenti ai due numeri interi per i quali si vuole calcolare l’MCD e restituisce un valore intero come risultato.

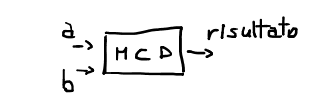
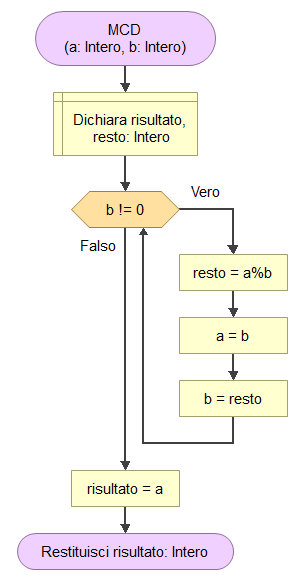
Per comprendere bene la struttura dell’agoritmo devi conoscere il concetto di struttura iterativa nella programmazione strutturata. L’algoritmo funziona nel seguente modo: per prima cosa si controlla che il valore inserito di b non sia 0.

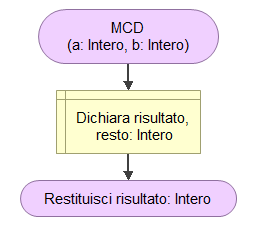
Fino a quando il valore di b è diverso da 0 l’algoritmo svolge i seguenti passi:

1. calcola il resto della divisione fra a e b e lo mette in una nuova variabile resto
2. mette b in a
3. mette resto in b

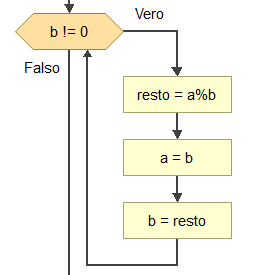
Al termine la variabile nella quale è contenuto il MCD è a. Vediamo l’algoritmo completo:

Verifica

Proviamo il funzionamento dell’algortimo sempre utilizzando i due numeri 4 e 6.

Come vediamo dal test effettuato nella variabile a è contenuto al termine proprio il numero 2 che risulta essere il Massimo Comun Divisore fra 4 e 6.

Implementazione

Possiamo a questo punto implementare la funzione che abbiamo precedentemente progettato. Proponiamo due implementazioni in linguaggio C++ e in linguaggio Python.

C++

#include <iostream>
#include <sstream>
#include <string>
#include <cstdlib>
#include <cmath>

using namespace std;

int MCD(int a, int b) {
    int risultato, resto;
    
    while (b != 0) {
        resto = a % b;
        a = b;
        b = resto;
    }
    risultato = a;
    
    return risultato;
}

Python

def MCD(a, b):
  while b != 0:
    resto = a % b
    a = b
    b = resto
  risultato = a

Vai a iterazioni